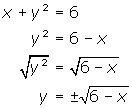NAVEGA A LAS MATEMATICAS

Objetivos de Aprendizaje

¿Que aprenderé?

1.- Funciones.

2.- Relaciones.

3.- Dominio.

4.- Contradominio.

5.- Imagen.

6.- Regla de correspondencia.

 

1.1 .- RELACIONES Y FUNCIONES.

Durante el transcurso de tu vida has necesitado vincular dos o más o fenómenos para entenderlos mejor y, así, transformarlos en una relaciónde correspondencia.

 

Para empenzar te explicaremos que es una Función y que es una Relacion.

 

Entender los conceptos de Relación y de Función es de suma importancia en Matemática.

Para lograr esa comprensión es necesario adentrarnos en la noción de Correspondencia, ya que esta tiene un papel fundamental en las relaciones y funciones.

Lo primero es entender que Correspondencia es equivalente a Relación. En nuestra lengua, decir “en relación a”, es equivalente a decir “corresponde a”.

Ejemplos:

En una tienda comercial, cada artículo está relacionado con su precio; o sea, a cada artículo le corresponde un precio.

En la guía telefónica, cada cliente está relacionado con un número; o sea, a cada nombre de la guía le corresponde un número.   

 

Definición de Relación y de Función.

En matemática, relacion es la correspondencia de un primer conjunto, llamado Dominio, con un segundo conjunto, llamado contradominio o codominio, de manera que a cada elemento del Dominio le corresponde uno o más elementos del contradominio o codominio.

Por su parte, una funcion es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del contradominio.

De las definiciones anteriores podemos deducir que todas las funciones son relaciones, pero no todas las relaciones son funciones.

También debemos agregar que toda ecuación es una Relación, pero no toda ecuación es una Función.

Todas las Relaciones pueden ser graficadas en el Plano Cartesiano.

Ver: Plano Cartesiano

Dados dos conjuntos A y B una relación definida de A en B es un conjunto de parejas ordenadas (par ordenado) que hacen verdadera una proposición; dicho de otro modo, una relación es cualquier subconjunto del producto cartesiano A x B

Ejemplo 1.

Si A = {2, 3}  y B = {1, 4, 5}, encontrar tres relaciones definidas de A en B.

Solución

El producto cartesiano de A x B está conformado por las siguientes parejas o pares ordenados:

                                        A x B = {(2, 1), (2, 4), (2, 5), (3, 1), (3, 4), (3, 5)}

Y cada uno de los siguientes conjuntos corresponde a relaciones definidas de A en B:

                                        R1 =  {(2, 1), (3, 1)}

                                        R2 =  {(2, 4), (2, 5), (3, 4), (3, 5)}

                                        R3 =  {(2, 4), (3, 5)}

La relación R1 se puede definir como el conjunto de pares cuyo segundo elemento es 1, esto es, R1 =  {(x, y) / y = 1}.

La relación R2 está formada por los pares cuyo primer componente es menor que el segundo componente, R2 = {(x, y) / x < y}

Y la relación R3 está conformada por todos los pares que cumplen con que el segundo componente es dos unidades mayor que el primer componente, dicho de otro modo, R3 =  {(x,  y) / y = x + 2}

Así, se puede continuar enumerando relaciones definidas a partir de A x B. Como se puede ver, la regla que define la relación se puede escribir mediante ecuaciones o desigualdades que relacionan los valores de x e y. Estas reglas son un medio conveniente para ordenar en pares los elementos de los dos conjuntos.

Ejemplo 2.

Dados los conjuntos C = {1, –3} y D = {2, 3, 6}, encontrar todos los pares ordenados (x, y) que satisfagan la relación

                                     R =  {(x, y) / x + y = 3}

Solución

El producto cartesiano de C x D está formado por los siguientes pares ordenados

                                      C x D = {(1, 2), (1, 3), (1, 6),  (–3, 2), (–3, 3),  (–3, 6)}

Las parejas ordenadas que satisfacen que la suma de sus componentes sea igual a 3 son:

                                     R =  {(1, 2), (–3, 6)}

Toda relación queda definida si se conoce el conjunto de partida, el conjunto de llegada y la regla mediante la cual se asocian los elementos. En el ejemplo anterior, el conjunto de partida corresponde al conjunto C, el conjunto de llegada es el conjunto D y la expresión  x + y = 3  es la regla que asocia los elementos de los dos conjuntos.

 

Dominio y Rango de una relación.

El dominio de una relación es el conjunto de preimágenes; es decir, el conjunto formado por los elementos del conjunto de partida que están relacionados. Al conjunto de imágenes, esto es, elementos del conjunto de llegada que están relacionados, se le denomina recorrido o rango.

Ejemplo 3 

Sea A = {1, 2, 3, 4}  y B = {4, 5, 6, 7, 8} y R la relación definida de A en B determinada por la regla “y  es el doble de x” o  “y = 2x”, encontrar dominio y rango de la relación.

Solución

El total de pares ordenados que podemos formar, o producto cartesiano es:

A x B =  {(1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (2, 4), (2, 5), (2, 6), (2, 7), (2, 8), (3, 4), (3, 5), (3, 6), (3, 7), (3, 8), (4, 4), (4, 5), (4, 6), (4, 7), (4, 8)}

Pero los pares que pertenecen a la relación R (y = 2x) son solo:

                                                 R = {(2, 4), (3, 6), (4, 8)}

En esta relación vemos que: “4 es el doble de 2”; esto es, “4 es la imagen de 2 bajo R”, dicho de otro modo, “2 es preimagen de 4”.

Así, el dominio y rango son:

                                              D = {2, 3, 4}

                                              Rg = {4, 6, 8}

Según lo que vemos, ¿Qué relación hay entre el Dominio y el conjunto de partida?

En el Dominio falta el elemento 1 del conjunto de partida, por lo tanto el Dominio es un subconjunto de A.

Otra pregunta: ¿Todo elemento del conjunto de llegada es elemento del rango?

La respuesta es no, pues en el rango faltan el 5 y el 7.

 

Representación gráfica de las relaciones.

 

Si f es una función real, a cada par (x, y) = (x, f(x)) determinado por la función f le corresponde en el plano cartesiano un único punto P(x, y) = P(x, f(x)). El valor de x debe pertenecer al dominio de definición de la función.

 

Como el conjunto de puntos pertenecientes a la función es ilimitado, se disponen en una tabla de valores algunos de los pares correspondientes a puntos de la función. Estos valores, llevados sobre el plano cartesiano, determinan puntos de la gráfica. Uniendo estos puntos con línea continua se obtiene la representación gráfica de la función.

 

x      1   2   3   4   5

f(x)  2   4   6   8   10
 

 

 

 

 

 

 

 

 

 

 

 

METODOS ALGEBRAICOS PARA LA OBTENCION DEL DOMINIO Y EL RANGO.

 

Para determinar analíticamente el dominio (valores de x que hacen que la y exista), lo primero que necesitamos es despejar de nuestra ecuación la variable dependiente (generalmente y). Lo segundo será analizar a cuál de los tres casos que describiremos más adelante se ajusta la ecuación despejada.

 

NOTA: Aunque en este curso nos centraremos en obtener el dominio (y luego el rango), en ecuaciones algebraicas cabe aclarar que la metodología es igualmente válida para las ecuaciones trascendentes: determinar qué valores puede tomar la variable independiente x.

 

Despejemos y de la ecuación de la parábola x+y2=6 que hemos venido utilizando como ejemplo:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

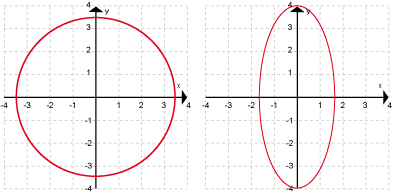
El dominio de esta circunferencia es el intervalo de valores entre -3.8 y 3.8, en tanto que el dominio de la elipse es el intervalo entre -1.7 y 1.7.

 

DETERMINAR EL RANGO DE MANERA ALGEBRAICA

En la determinación de las intersecciones y las simetrías seguramente te diste cuenta que trabajamos un mismo algoritmo y según el eje analizado (x o y) la condición se modificó: Hicimos y=0 para la intersección con el eje x, e hicimos x=0 para las intersecciones con el eje y. Cambiamos x por –x para investigar la simetría con respecto al eje de las ordenadas (y), y cambiamos la y por –ypara la simetría con respecto al eje de las abscisas (x). Así que si para el dominio despejamos la variable dependiente y, para el RANGO habrá que despejar x y, de manera análoga al dominio, analizar cuál de los tres casos tenemos para determinar el rango.

 

 

1.2 CLASIFICACION DE LAS FUNCIONES.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

CLASIFICACIÓN SEGÚN LA VARIABLE X:

En primer lugar clasificaremos las funciones dependiendo del carácter de la variable independiente x en dos tipos: algebraicas y trascendentes.
*Funciones algebraicas: Este tipo de funciones corresponden a ecuaciones polinómicas , donde se pueden efectuar operaciones en las que interviene la variable independiente, como la suma, la resta, la multiplicación, la división, la potencia y la raíz.
Dentro de las funciones algebraicas nos encontramos:
- Funciones constantes: donde la función viene definida por una constante y no interviene la variable independiente: y=f(x)=k
-Funciones lineal: La representación de este tipo de funciones es una recta que pasa por el origen de coordenadas: y=mx+n.
-Función afín: Esta función se trata de un caso general de la anterior, ya que se trata de una recta cualquiera del plano: y= mx
-Función cuadrática: Viene expresada por una función polinómica de segundo grado, como era de esperar, y su representación es una parábola.
-Funciones racionales: Se expresan mediante el cociente de polinomios.
-Funciones radicales: Vienen dadas por la raíz de una expresión polinómica.
-Funciones a trozos: Son funciones definidas por una función distinta en cada intervalo (o trozo) que se considere.

 

*Funciones trascendentes: Cuando la variable independiente, x, forma parte del exponente o da la base de un logaritmo; o simplemente se ve afectada por una función, como puede ser en la trigonometría, entonces hablamos de funciones trascendentes.
Dentro de las funciones trascendentes están:
-Función exponencial: Como su nombre indica es una función en la que la variable independiente se encuentra en el exponente y cuya base es un número real. Por tanto, recibe el nombre de función exponencial de base a y exponente x.
-Función logarítmica: La inversa de la función exponencial recibe el nombre de función logarítmica, por tanto, devuelve el número al que tendríamos que elevar la base a, para obtener nuestra variable independiente. (En este caso la variable independiente nos da el valor de la función exponencial)
-Funciones trigonométricas:Las funciones trigonométricas se obtienen cuando ampliamos el concepto de razones trigonométricas a los números reales. Por lo que hay el mismo número de funciones trigonométricas que de razones trigonométricas: y=senx, y=cosx, y=sec x, etc.

En la siguiente imagen, tenemos una clasificación de lo que acabamos de estudiar.

 

CLASIFICACIÓN SEGÚN LA DEFINICIÓN
Según nos venga dada la definición de la función también podemos establecer una clasificación:
-Función explícita: Cuando podemos obtener los valores de y directamente dando valores a nuestra variable independiente, es decir, cuando la variable y está despejada.

-Función implícita: Cuando, al contrario que en el caso anterior, tenemos que realizar operaciones para halla el valor de la y una vez que le hemos dado un valor a la x: 3x+2y=1

 

 RECOMOCIMIENTO GRÀFICO DE UNA RELACIÒN O DE UNA FUNCIÒN

 

Cuando la cantidad independiente (entrada) y la cantidad dependiente (salida) son ambas números reales, una función puede ser representada por una gráfica de coordenadas. El valor independiente se grafica en el eje x y el valor dependiente es trazado en el eje y. El hecho de que cada valor de entrada tiene exactamente un valor de salida significa que las gráficas de funciones tienen ciertas características. Para cada entrada (coordenada x) en la gráfica, habrá exactamente una salida (coordenada y).

 

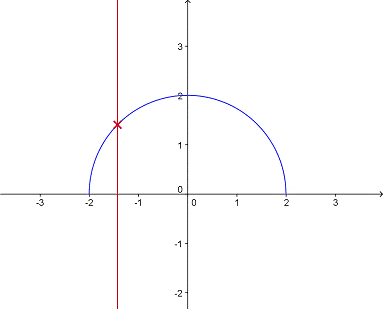
Por ejemplo, la gráfica de ésta función, dibujada en azul, parece un semicírculo. Sabemos que y es una función de x porque por cada coordenada x hay exactamente una coordenada y.

 

 

 

 

 

 

 

 

 

 

Si trazamos una línea vertical a través de la gráfica, sólo intersecta la función. Una vez para cada valor de x. Esto es válido sin importar por dónde la línea es trazada. Dibujar una línea sobre una gráfica es una buena forma de determinar si nos muestra una función.

 

Compara la gráfica anterior con ésta, que parece un círculo azul. La relación no puede ser una función, porque a cada coordenada x le corresponden dos coordenadas y.

 

Cuando una línea vertical es trazada sobre la gráfica de ésta relación, la intersecta en más de un valor de x. Si la gráfica muestra dos o más intersecciones con una línea vertical, entonces una entrada (coordenada x) puede tener más de una salida (coordenada y), y y no es una función de x.