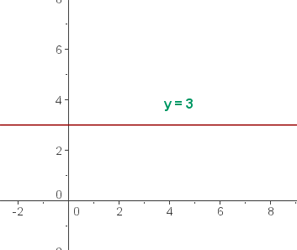Bloque II. Operaciones con distintos tipos de funciones.

 

Objetivos de Aprendizaje

¿Que aprenderé?

1.- Funcion inversa.

2.- Funcion escalonada.

3.- Funcion valor absoluto.

4.- Funcion identidad.

5.- Funcion constante.

 

 

2.1 Funcion inversa

Se llama función inversa o reciproca de f a otra función f−1 que cumple que:

Si f(a) = b, entonces f−1(b) = a.

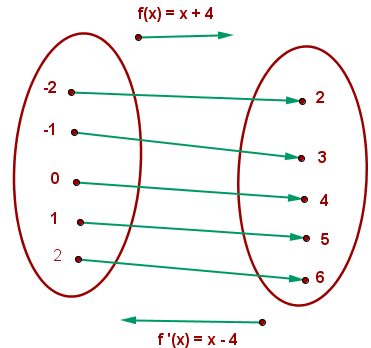
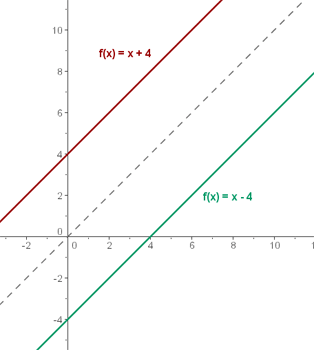
Veamos un ejemplo a partir de la función f(x) = x + 4

 

 

 

Podemos observar que:

-El dominio de f−1 es el recorrido de f.

-El recorrido de f−1 es el dominio de f.

-Si queremos hallar el recorrido de una función tenemos que hallar el dominio de su función inversa.

-Si dos funciones son inversas su composición es la función identidad.

(f o f−1) (x) = (f−1 o f) (x) = x

-Las gráficas de f y f-1 son simétricas respecto de la bisectriz del primer y tercer cuadrante.

 

Calculo de la Funcion Inversa

1.Se escribe la ecuación de la función con x e y.

 

2.Se despeja la variable x en función de la variable y.

 

3.Se intercambian las variables.

 

Ejemplos

Calcular la función inversa de:

Vamos a comprobar el resultado para x = 2

 

Funciones especiales

En la teoria de funciones, se presetan algunos cuyo comportamiento es diferente en relacion a todas las

funciones algebraicas. Sera necesario que tengas presente el estudio de su dominio y rango para que

poamos descubrir en qué situacion de la vida cotidiana se aplica.

 

 

FUNCION CONSTANTE

La función constante es del tipo:

y = n

El criterio viene dado por un número real.

La pendiente es 0.

La gráfica es una recta horizontal paralela a al eje de abscisas.

 

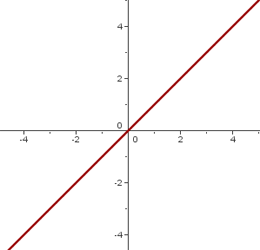
FUNCION IDENTIDAD

 

La función identidad es del tipo:

f(x) = x

Su gráfica es la bisectriz del primer y tercer cuadrante.

Por tanto la recta forma con la parte positiva del eje de abscisas un ángulo de 45º y tiene de pendiente: m = 1.

 

FUNCION VALOR ABSOLUTO

 El valor absoluto està definido como la distancia que existe entre el 0 y el nùmero en cuentiòn, lo que implica que el resultado siempre serà positivo. 

 

Para graficar la funciòn del valor absoluto, primero se grafica de y=x para los valores positivos de x y despuès y=-x para valores menores a 0.

 

FUNCIONES SECCIONADAS

 Tambièn son llamadas funciones definidas por partes, pues estàn formadas por un conjunto de funciones con diferentes comportamientos o secciones en distintas partes de su diminio. Asimismo, dependiendo del intervalo que se analice, una funciòn seccionada puede tener una secciòn continua y otra discontinua.

 

TRASLACION DE GRÁFICAS DE FUNCIONES

Los desplazamientos verticales y los desplazamientos horizontales en las ecuaciones cuadráticas  esta de terminados a partir de origen o la coordenada (0,0).

VERTICAL

Si la gráfica se mueve hacia arriba o hacia abajo el valor de b y su signo son iguales.

HORIZONTAL

Si el desplazamiento es hacia los lados, el signo de uno de los términos será contrario.

EJEMPLO:

La función f(x) = (x +2)² + 3

El vértice de esta función estará ubicado en la coordenadas (- 2 , 3 )

 

REFLEXIÓN CON RESPECTO AL EJE EQUIS

Una forma de trasladar las funciones desde el origen es una reflexión o un reflejo de las coordenadas que determinan la grafica.

Se a la  función y = x² sabemos que es una grafica curva que abre hacia arriba, pero si esta función cambia un poco con el signo contrario a ser y = – x² entonces se muestra una grafica distinta.

Vemos en esta grafica la función que da origen a la traslación es positiva y la que se refleja es negativa. Una forma de recordar como queda la trasformación es que cuando la función cuadrática es positiva resulta “feliz” y si es negativa, resulta una gráfica “triste”.

 

Estas transformaciones de una función son las básicas. como hemos dicho, cuando la gráfica se mueve, la ecuación algebraica sufre también sus cambios.