
Bloque III. Funciones Polinomiales de Grados cero uno y tres.
Objetos de Aprendizaje:
1.-Modelos general de las funciones polinomiales.
2.-Representacion de graficas de grado cero uno y dos.
3.-Caracteristicas de las funciones polinomilaes.
3.1 Funciones Polinomiales de una variable.
La función polinomial se llama así porque generalmente su expresión algebraica es un polinomio; su forma general es:
f(x) = anxn + an–1xn–1 + an–2xn–2 + ... +a0x0
Las funciones polinómicas son aquellas cuya expresión es un polinomio, como por ejemplo:
f(x)=3x4-5x+6 se trata de funciones continuas cuyo dominio es el conjunto de los números reales.
En la figura se pueden ver las gráficas de las funciones polinómicas de grado menor que 3.
Observa la forma según su grado:
Las de grado cero como f(x)=2, son rectas
horizontales;
Las de grado uno, como f(x)=2x+4, son rectas
oblicuas;
Las de grado dos, como f(x)=2x2+4x+3, son
parábolas cuyo eje es paralelo al de ordenadas.

La linea Recta
La linea recta se define como un lugar geometrico, formado por un conjunto de puntos que mantienen la misma direccion o inclinacion, es decir el angulo de inclinacion que forman es el mismo para toda la grafica.
La ecuación GENERAL de una línea recta tiene la forma:
y = mx + b
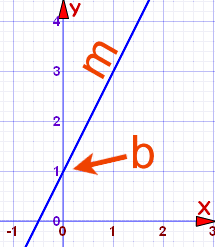
Ejemplo 1:
m=2/1=2
b=2
por tanto y=2x+1
Dominio y Rango de Una Función Cuadrática.
-El DOMINIO de una función cuadrática incluye a todos los números reales, ya que no hay ningún cociente que pueda derivar en una entre cero ni la posibilidad que exista una raíz negativa.
-El RANGO estará determinado por el valor de la coordenada y del vértice, así como por la función, es decir, si se trata de una función cuadrada cóncava hacia arriba o hacia abajo.
Ejemplo.
=χ²+4x-5
Cuando el término cuadrático es positivo nos indica que es una parábola abierta hacia arriba.
b)y=-4χ²-x+3
En este caso como el coeficiente cuadrático es negativo la parábola es abierta pero hacia abajo.
Ejercicios.
1.- y=4χ²-5x+1
2.- y=-5χ²-3x
Modelos cuadráticos.
Los modelo cuadrático son problemas en los cuales hay que encontrar un valor máximo y un valor mínimo . Se deben de considerar algunos puntos como los sig.
1.-Plantear la ecuación necesariamente de segundo grado.
2.-Calcular el valor de la vértice para encontrar la coordenada de la variable independiente en el que se presenta un cambio de sentido.
Ejemplo.
Un bateador le pega a una pelota, la cual describe una trayectoria parabólica definida por h=-3t2+6t+9¿En qué tiempo alcanzara su máxima altura?
La ecuación h=-3t2+6t+9 es una parábola abierta hacia abajo por lo que su vértice representa un máximo y sus coordenadas serian v (t,h).
Se sustituye los valores de la formula y nos quedaría.
(-(6) 4(-3)(9)-(6)2
v(------,---------------)
2(-3) 4(-3)
Por tanto, el vértice es v(1,12) esto es el valor máximo al que llega la pelota (12m en el tiempo t=1s).
Las coordenadas del vertices se ontienen mediante las siguientes relaciones:
v(-b/2a, 4ac-b2)/4a)

Dominio y Rango de una funcion cuadratica
El Dominio de una cuadratica incluye todos los numeros reales, ya que no hay ningun cociente que pueda derivar en una division entre cero ni la posibilidad que exista en una raiz.
El Rango esta determinado por el valor de la coordenada y del vertice, asi como por la funcion, es decir, si esta se trata de una funcion cuadrada concava hacia arriba o hacia abajo.
Ejemplo:
|1.- Determinar el rango de las siguiente funcion cuadratica.
a) y=x2+4x-5
Determinamos las coordenadas que son: v(-2,-9). como es una parabola concava hacia arriba, su rango estara determinado desde -9 hasta infinitp esto es igual a:
R=(y ER/y>-9)
B) y=-4x2-x+3
Debido a que el coeficente del termino cuadratico es negativo, la parabola abre hacia abajo,por lo que los valores del rango estan por debajo de las coordenadas las cuales son: v(-1/8, 16/49)
R=(yer/y<16/40)



