NAVEGA A LAS MATEMATICAS
BLOG DE APRENDIZAJE EN LINEA.
Bloque VI. Funciones Racionales
Objetos de Aprendizaje:
1.-Funcion racional.
2.-Dominio de definicion.
3.-Asintotas racionales.
4.-Criterios de existencias de las asintotas horizontales
Concepto de funcion racional:notacion y carcterizacion
Cuando una funcion esta formada por el coeficiente de dos funciones polinomiales se denomina la funcion racional R(x), lo cual podemos denotar de la siguiente manera :
En donde A(x) y D(x) son funciones polinimiales. se considera funcion racional siempre y cuando D(x) bo valaga cero en ningun instante y que el polinomio R(x) sea irreducible, es decir no pueda factorizarse.
Al dibujar su gráfica obtenemos una hipérbola equilátera.
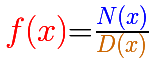
Dominio y Rango:INTERVALOS
El dominio de una funcion racional es el conjunto de todos aquellos valores que pueden asignarse a la variable x que no den como resultado una division entre cero, por lo que dependere de cada funcion la asignacio de los intervalos del dominio.
Ejemplo:
Encontremos el dominio de la sigeuinte funcion:
4x-5
a) y=
6x-6
para encontrar el dominio de una funcion, debemos plantear que el denominador debe ser diferente de cero, entonces:
6x-6 0
Al despejar tenemos:
x === 6
x === 6/6
x === 1
Por lo tanto, el dominio es:
D{xE R/ x == 1}
Para determinar el rango de una funcion racional es necesario graficar, como se sabe es caracteristoca de cada funcion.
Asintotas verticales, horizontales y oblicuas.
Cuando la curva de una grafica tiende all infinito, se puede trazar una recta cuya distancia con la curva tienda a cero y que se aleja indefinidamente del origen, a esta recta se le conoce como asintota. La asintota se define como la tangente a la curva en el infinito.
Asintota vertical:
Las asintotas verticales corresponden al valor de x en el denominador se hace cero. Para encontrar su ecuacion, se iguala el denominador a cero y se despeja x.
Asintota horizontal:
Las funciones racionales no necesariamente tienen asintota horizontal. Para encontrar su ecuacion, se divede la funcion entre el valor de x con mayor exponente, luego se susitituye la x por infinito y se resuelve la ecuacion.
Asintota oblicua:
si en la funcion racional R(x)=A(x)/D(x) es una unidad mas grande que D(x), la funcion presenta una asintota oblicua. Para encontrar las ecuaciones, se dvide A(x) entre D(x); el cociente tendra la forma de la ecuacion canonica de la recta y=mx+b.
